Các nhà nghiên cứu đã đạt được một bước tiến lớn trong hình học quang phổ bằng cách chứng minh một trường hợp đặc biệt của giả thuyết Bolya liên quan đến các giá trị riêng của đĩa. Công việc của họ, kết hợp sự tao nhã về mặt lý thuyết với những ứng dụng thực tế tiềm năng, làm nổi bật giá trị phổ quát và vẻ đẹp nghệ thuật của nghiên cứu toán học. Tín dụng: SciTechDaily.com
Một trong những giáo sư và cộng sự của ông đã chứng minh phỏng đoán của Polya về các giá trị riêng của đĩa, một bài toán khó trong toán học.
Có thể suy ra hình dạng của cái trống từ âm thanh nó tạo ra không?
Đây là loại câu hỏi mà Iosif Poltrovic, giáo sư Khoa Toán và Thống kê tại Đại học Montreal, thích hỏi. Poltrovic sử dụng hình học quang phổ, một nhánh của toán học, để hiểu các hiện tượng vật lý liên quan đến sự truyền sóng.
Bước đột phá trong ước lượng toán học
Mùa hè năm ngoái, Poltrović và các cộng tác viên quốc tế của ông – Nikolai Filonov, Michael Levitin, và David Scherr – đã chứng minh một trường hợp đặc biệt của phỏng đoán hình học quang phổ nổi tiếng được nhà toán học nổi tiếng người Mỹ gốc Hungary George Polya đưa ra vào năm 1954.
Việc ước tính liên quan đến việc ước tính tần số của hình trụ tròn, hay nói theo thuật ngữ toán học là các giá trị riêng của đĩa.
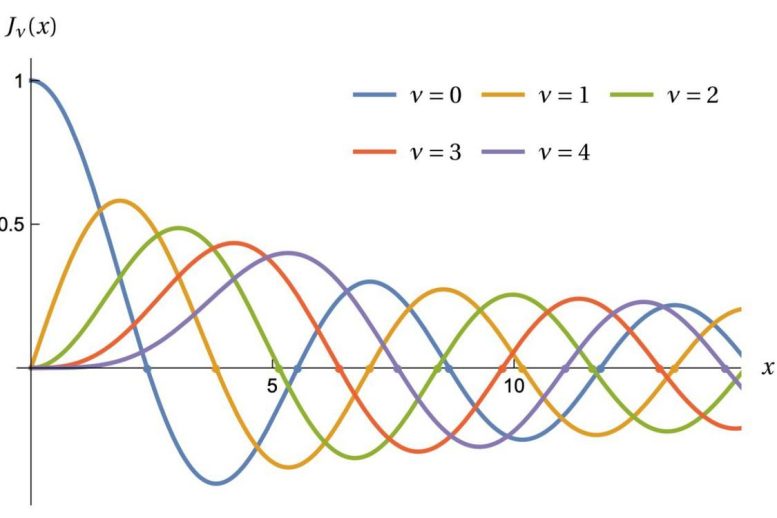
Sơ đồ này thể hiện các hàm Bessel, trong đó các chấm tương ứng với tần số của âm thanh do một chiếc trống tròn tạo ra. Tín dụng: Michael Levitin
Chính Polya đã xác nhận phỏng đoán của mình vào năm 1961 về các hình cầu tạo nên mặt phẳng, chẳng hạn như hình tam giác và hình chữ nhật. Cho đến năm ngoái, dự đoán này chỉ được biết đến với những trường hợp này. Chiếc đĩa, mặc dù có vẻ đơn giản nhưng vẫn khó nắm bắt.
Poltrovic nói: “Hãy tưởng tượng một tầng vô tận được bao phủ bởi những viên gạch có hình dạng giống nhau khớp với nhau để lấp đầy không gian”. “Chúng có thể được lát bằng hình vuông hoặc hình tam giác, nhưng không được lát bằng đĩa. Đĩa thực sự không phải là hình dạng thích hợp để lát gạch.
Tính phổ quát và tác động của toán học
Trong một bài báo đăng trên tạp chí thể thao vào tháng 7 năm 2023 Những phát minh toán họcCác nhà nghiên cứu đã chỉ ra rằng phỏng đoán của Bolya là đúng đối với một chiếc đĩa, một trường hợp được coi là đặc biệt khó khăn.
Mặc dù kết quả của họ chủ yếu có giá trị lý thuyết, phương pháp chứng minh của họ có ứng dụng trong toán học tính toán và tính toán số. Các tác giả hiện đang nghiên cứu phương pháp này.
Joseph Poltrovic
Poltrovic nói: “Mặc dù toán học là một môn khoa học cơ bản, nhưng nó cũng tương tự như thể thao và nghệ thuật ở một khía cạnh nào đó.
“Cố gắng chứng minh một phỏng đoán lâu đời là một môn thể thao. Tìm ra lời giải hay là một nghệ thuật. Trong nhiều trường hợp, những khám phá toán học đẹp đẽ rất hữu ích, bạn chỉ cần tìm được ứng dụng phù hợp.”
Tham khảo: “Giả thuyết Polya cho các quả cầu Euclide” của Nikolai Filonov, Michael Levitin, Iosif Poltrovic và David A. Chia sẻ, ngày 5 tháng 6 năm 2023, Những phát minh toán học.
doi: 10.1007/s00222-023-01198-1